Arithmetic

MLModule

genre

Arithmetic

authors

Lennart Tautz, Ola Friman

package

FMEstable/ReleaseMeVis

dll

MLArithmetic

definition

MLArithmetic.def

see also

Arithmetic0, Arithmetic1, Arithmetic2, ComplexArithmetic1, ComplexArithmetic2, SoCalculator, Calculator, TypeArithmetic1, TypeArithmetic2, TestPattern, ConstantImage

keywords

arithmetic, expression, evaluation, calculator, calculation, voxelwise, image, operation, mathematics, logic, log, exp, abs, sin, cos, tan, min, max, add, subtract, minus, multiply, divide, scalar, vector, complex, quaternion, matrix

Purpose

This module performs voxel-wise arithmetic operations with up to ten input images. The output is the processed image according to the entered arithmetic expression and chosen variables.

Usage

Enter the arithmetic expression you want to apply to the input images. You can specify additional variables in the respective fields. The expression is evaluated voxel-wise. Input images must have the same extent, otherwise no output will be calculated. The min/max values of the output image will be the minimum and maximum, respectively, of the inputs’ min/max values. The voxel-to-world matrix will be taken from the first valid input image. Note that for the aforementioned properties all connected and valid images are considered. This holds for the output type as well (see below), and in particular for the constant expressions that don’t use image variables. This module supports multi-threading.

Output type

The output type is chosen so that it can hold the result. It is possible to combine input images of different types to a certain degree, as long as the types are reasonably compatible. Furthermore, if the expression will result in fractional results (i.e. by using fractional constants or trigonometric functions), the output type will changed to the next higher type able to hold such results. This may lead to a loss of precision when using MLint64 as input type. Note that due to the determination of the output type from the input types, functions such as real, imag and arg retain the complex input type, but exhibit an imaginary part of zero. If the expression uses unary minus, the type is likewise changed so that it can hold signed values. If the expression uses bitwise logical functions, the type is changed to an unsigned integer type. If variables are used, the type is changed so that it can hold their values. If the type requirements of the expression, the input images and the variables cannot be met by any type, no output will be calculated.

The following table summarizes the conditions that change the output type when met.

Condition

Output type is at least

Decimal number (e.g. ‘1.2’)

MLfloat

Constant ‘pi’

MLdouble

Double variable (d1-d12)

MLdouble
Trigonometric and certain other functions:
cos, sin, tan, acos, asin, atan,
cosh, sinh, tanh, exp, log,
log10, log2, sqrt, root

MLfloat

Unary minus (e.g. ‘-i1’)

MLint8

Bitwise functions

MLuint8

Output page extent

The page extent of the output image will be copied from the left-most image that is connected. The page extent is never modified. This table exemplifies some use cases:

Image0 Page Extent

Image1 Page Extent

Expression

Output Page Extent

48x16

32x32

a + b

48x16

48x16

48x16

a + b

48x16

48x16

32x32

b

48x16

Combination of input types

Generally, the inputs must be of the same type. Combinations of different types, e.g., vectors and scalars or matrices and vectors, are not possible. Scalar types can be arbitrarily combined, but certain combinations may lead to loss of precision or information. Other types that are compatible internally, such as complexf and complexd, or Vector16 and Vector64, may be used together under the same conditions. Scalar multiplication and division of vectors (vec and vecf types) and matrices (mat and matf types) is realized through component-wise multiplication and division, respectively, with a vector/matrix containing the value of the scalar in all components.

Support of registered types

The dimension of input and output types is always the same. This means that you cannot, for example, calculate the norm of a vector. Instead, many functions that are available for registered types will be calculated component-wise (e.g. cos on each component instead of cos on a whole vector). However, many functions are not supported at all for certain types. Note that there will be no error message if you try to use incompatible types and functions. The output image will simply not be computed. See the tables below for more information.

This table shows the available types and their association to type groups (for ease of read):

Type group

ML types

Standard
MLint8, MLuint8, MLint16, MLuint16, MLint32, MLuint32, MLint64, MLuint64,
MLfloat, MLdouble

Complex

complexf, complexd, complexld

Quaternion

quaternionf, quaterniond, quaternionld

Vector
vec2, vec3, vec4, vec5, vec6, vec7, vec8, vec9, vec10, vec16, vec32, vec64,
vecf2, vecf3, vecf4, vecf5, vecf6, vecf7, vecf8, vecf9, vecf10, vecf16,
vecf32, vecf64

Matrix

mat2, mat3, mat4, mat5, mat6, matf2, matf3, matf4, matf5, matf6

This table shows which type group supports which functions. While ‘Y’ and ‘-’ indicate (native) support and no support, respectively, ‘C’ indicates support by means of component-wise calculation.

Function

Standard

Complex

Quaternion

Vector

Matrix

Basic functions

+

Y

Y

Y

Y

Y

-

Y

Y

Y

Y

Y

*

Y

Y

Y

C

C

/

Y

Y

-

C

C

%

Y

-

-

-

-

- (unary)

Y

Y

Y

Y

Y

min

Y

-

-

C

C

max

Y

-

-

C

C

diff

Y

-

Y

C

C

abs

Y

Y

C

C

C

sgn

Y

-

C

C

C

absmin

Y

-

-

C

-

absmax

Y

-

-

C

-

Trigonometric functions

cos

Y

-

-

C

C

sin

Y

-

-

C

C

tan

Y

-

-

C

C

cosh

Y

-

-

C

C

sinh

Y

-

-

C

C

tanh

Y

-

-

C

C

acos

Y

-

-

-

-

asin

Y

-

-

-

-

atan

Y

-

-

-

-

atan2

Y

-

-

-

-

Exponential and logarithmic functions

pow

Y

Y

-

C

-

sqr

Y

Y

-

C

-

root

Y

-

-

-

-

sqrt

Y

Y

-

C

C

exp

Y

-

-

C

C

log

Y

-

-

C

C

log10

Y

-

-

C

C

log2

Y

-

-

C

C

Logical functions

==

Y

Y

Y

Y

Y

!=

Y

Y

Y

Y

Y

<

Y

-

-

C

C

>

Y

-

-

C

C

<=

Y

-

-

C

C

>=

Y

-

-

C

C

and

Y

-

-

-

-

or

Y

-

-

-

-

xor

Y

-

-

-

-

imp

Y

-

-

-

-

!

Y

-

-

-

-

& [1]

Y

-

-

-

-

| [1]

Y

-

-

-

-

^ [1]

Y

-

-

-

-

if

Y

-

-

-

-

Rounding functions

floor

Y

-

-

C

C

ceil

Y

-

-

C

C

round

Y

-

-

C

C

Functions on complex values

arg

-

Y

-

-

-

real

-

Y

-

-

-

imag

-

Y

-

-

-

conj

-

Y

-

-

-

Functions on vector and matrix values

.*

-

-

-

Y

Y

./

-

-

-

Y

Y

norm

-

-

-

Y

-

dot

-

-

-

Y

-

cross

-

-

-

Y [2]

-

length

-

-

-

Y

-

Operator precedence

The following table lists the precedence of infix functions, where a higher precedence group means higher precedence.

Precedence group

Functions

1

imp

2

or / ||

3

xor

4

and / &&

5

|

6

^

7

&

8

==, !=

9

<, >, <=, >=

10

+, -

11

*, /, %, .*, ./

Details

The arithmetic language over images used in this module combines functions and arguments to form an arithmetic expression.

If you enter an invalid expression, a message indicating the error will be displayed in the module panel.

Functions

Function

Syntax

Description

Basic functions

+

a + b

Addition

-

a - b

Subtraction

*

a * b

Multiplication

/

a / b
Division
If b is zero, a domain error occurs

%

a % b

Modulo

-

- a

Unary minus (invert)

min

min(a, b)
Minimum of arguments
Applied component-wise to vector and matrix values

max

max(a, b)
Maximum of arguments
Applied component-wise to vector and matrix values

diff

diff(a, b)

Difference (absolute value after subtraction)

abs

abs(a)

Absolute value

sgn

sgn(a)

Signum (result is 1 for positive values, 0 for zero and -1 for negative values)

absmin

absmin(a, b)
Returns the argument that has the minimum absolute value
If the absolute values are equal, the minimum is returned
Applied component-wise to vector values

absmax

absmax(a, b)
Returns the argument that has the maximum absolute value.
If the absolute values are equal, the maximum is returned
Applied component-wise to vector values

Trigonometric functions

cos

cos(a)

Cosine

sin

sin(a)

Sine

tan

tan(a)

Tangent

cosh

cosh(a)

Hyperbolic cosine

sinh

sinh(a)

Hyperbolic sine

tanh

tanh(a)

Hyperbolic tangent

acos

acos(a)
Inverse cosine
If a is outside of range [-1;1], a domain error occurs

asin

asin(a)
Inverse sine
If a is outside of range [-1;1], a domain error occurs

atan

atan(a)

Inverse tangent

atan2

atan2(y, x)

atan2 (note reversed argument order)

Exponential and logarithmic functions

pow

pow(a, b)

a raised to the power of b

sqr

sqr(a)

a squared

root

root(a, b)
b-th root of a
If b is zero, a domain error occurs

sqrt

sqrt(a)
Square root
If a is negative, a domain error occurs

exp

exp(a)

e raise to the power of a

log

log(a)
Natural logarithm
If a is zero or negative, a domain error occurs

log10

log10(a)
Decadic logarithm
If a is zero or negative, a domain error occurs

log2

log2(a)
Binary logarithm
If a is zero or negative, a domain error occurs

Logical functions

==

a == b

Equality

!=

a != b

Inequality

<

a < b
a is less than b
Applied component-wise to vector and matrix types
For those types, the comparison is true if all components compare true

>

a > b
a is greater than b
Applied component-wise to vector and matrix types
For those types, the comparison is true if all components compare true

<=

a <= b
a is equal to or less than b
Applied component-wise to vector and matrix types
For those types, the comparison is true if all components compare true

>=

a >= b
a is equal to or greater than b
Applied component-wise to vector and matrix types
For those types, the comparison is true if all components compare true
and
&&
a and b
a && b

Logical AND
or
||
a or b
a || b

Logical OR

xor

a xor b

Logical XOR (exclusive OR)

imp

a imp b

Logical implication

!

! a

Logical NOT

&

a & b

Bitwise AND

|

a | b

Bitwise OR

^

a ^ b

Bitwise XOR (exclusive OR)

if

if(a, b, c)

Conditional expression | This is replaced by (a)*(b)+!(a)*(c) internally for now.

Rounding functions

floor

floor(a)

Floor value

ceil

ceil(a)

Ceil value

round

round(a)

Rounded value

Functions on complex values

arg

arg(a)

Argument of complex value | Result is a complex value where both parts are set to the result

real

real(a)

Real part of complex value | Result is a complex value where both parts are set to the result

imag

imag(a)

Imaginary part of complex value | Result is a complex value where both parts are set to the result

conj

conj(a)

Complex conjugate of complex value

Functions on vector and matrix values

.*

a .* b

Component-wise multiplication

./

a ./ b

Component-wise division

norm

norm(a)

Normalize a to unit vector

dot

dot(a, b)
Dot product
Result is a vector where all components are set to the result

cross

cross(a, b)
Cross product
Available only for vec3 and vecf3 types

length

length(a)
Length of vector
Result is a vector where all components are set to the result

Arguments

A function argument can be one of the following:

  • An input image (a through j). The expression is evaluated for every voxel of the indicated input image.

  • A literal value (for example 5, -5 or 1.3, but not 2.). When the expression is evaluated over a multi-component type such as vectors or matrices, a literal number is converted to a value of that type where all components are set to that number.

  • A built-in constant: pi

  • A variable (i1-i6, d1-d12). The variable is evaluated to the value set in the module panel.

  • A coordinate variable (cx, cy, cz, cc, ct, cu). During evaluation, these variables hold the dimensional coordinates of the current voxel.

Legacy Support

The variables f1-f6 and ld1-ld6 redirect to d1-d6 and d7-d12 both as fields and as variables in the expression.

Tips

Pure constant expressions

You can create a constant image by omitting any input image arguments from the expression and enabling the data type and image extend setting fields. In some cases this might be better than using a ConstantImage or TestPattern as input image for the Arithmetic.

Setting min/max values

Typically, the min value of the output image is the minimum of the min values all used input images (likewise the maximum of all values for the max value). This heuristic will usually produce somewhat reasonable, but still wrong min/max values. If you or your application know the exact (or desired) values, you should set them manually in the Settings tab.

Input connectors

If less than ten inputs are required, the open connectors can be hidden by setting an appropriate number here. If a connector is hidden by this, it is disconnected.

Windows

Default Panel

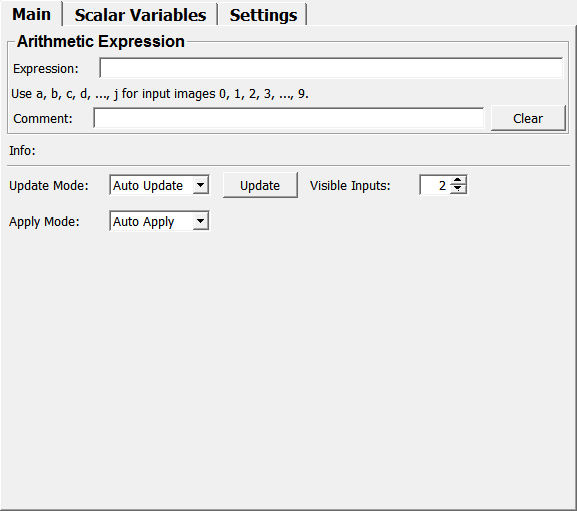
../../../Modules/ML/MLArithmetic/mhelp/Images/Screenshots/Arithmetic._default.png

Input Fields

The module has ten image inputs and one output image. Inputs ‘c’ and above are hidden by default.

input0

name: input0, type: Image

Image ‘a’ in expression

input1

name: input1, type: Image

Image ‘b’ in expression

input2 (hidden)

name: input2, type: Image

Image ‘c’ in expression

input3 (hidden)

name: input3, type: Image

Image ‘d’ in expression

input4 (hidden)

name: input4, type: Image

Image ‘e’ in expression

input5 (hidden)

name: input5, type: Image

Image ‘f’ in expression

input6 (hidden)

name: input6, type: Image

Image ‘g’ in expression

input7 (hidden)

name: input7, type: Image

Image ‘h’ in expression

input8 (hidden)

name: input8, type: Image

Image ‘i’ in expression

input9 (hidden)

name: input9, type: Image

Image ‘j’ in expression

Output Fields

output0

name: output0, type: Image

Result of evaluated expression

Parameter Fields

Field Index

Apply Mode: Enum

d6: Double

i4: Integer

Clear Variables: Trigger

d7: Double

i5: Integer

Comments: String

d8: Double

i6: Integer

d1: Double

d9: Double

Info: String

d10: Double

Data Type: Enum

Max: Float

d11: Double

Expression: String

Min: Float

d12: Double

Expression Comment: String

Set data type: Bool

d2: Double

Handling on Domain Error: Enum

Set min/max values: Bool

d3: Double

i1: Integer

Update: Trigger

d4: Double

i2: Integer

Update Mode: Enum

d5: Double

i3: Integer

Visible Inputs: Integer

Visible Fields

Expression

name: expression, type: String

Enter an expression.

i1

name: i1, type: Integer, default: 0, deprecated name: intConstant0

Integer variable i1

i2

name: i2, type: Integer, default: 0, deprecated name: intConstant1

Integer variable i2

i3

name: i3, type: Integer, default: 0, deprecated name: intConstant2

Integer variable i3

i4

name: i4, type: Integer, default: 0, deprecated name: intConstant3

Integer variable i4

i5

name: i5, type: Integer, default: 0, deprecated name: intConstant4

Integer variable i5

i6

name: i6, type: Integer, default: 0, deprecated name: intConstant5

Integer variable i6

d1

name: d1, type: Double, default: 0, deprecated name: ld1,longDoubleConstant0

Double variable d1

d2

name: d2, type: Double, default: 0, deprecated name: ld2,longDoubleConstant1

Double variable d2

d3

name: d3, type: Double, default: 0, deprecated name: ld3,longDoubleConstant2

Double variable d3

d4

name: d4, type: Double, default: 0, deprecated name: ld4,longDoubleConstant3

Double variable d4

d5

name: d5, type: Double, default: 0, deprecated name: longDoubleConstant4,ld5

Double variable d5

d6

name: d6, type: Double, default: 0, deprecated name: ld6,longDoubleConstant5

Double variable d6

d7

name: d7, type: Double, default: 0, deprecated name: floatConstant0,f1

Double variable d7

d8

name: d8, type: Double, default: 0, deprecated name: f2,floatConstant1

Double variable d8

d9

name: d9, type: Double, default: 0, deprecated name: floatConstant2,f3

Double variable d9

d10

name: d10, type: Double, default: 0, deprecated name: floatConstant3,f4

Double variable d10

d11

name: d11, type: Double, default: 0, deprecated name: floatConstant4,f5

Double variable d11

d12

name: d12, type: Double, default: 0, deprecated name: floatConstant5,f6

Double variable d12

Min

name: minValue, type: Float, default: 0

New min value of the output image.

Max

name: maxValue, type: Float, default: 1

New max value of the output image.

Set min/max values

name: setMinMaxValues, type: Bool, default: FALSE

If checked, the min/max values of the output image are set to the indicated values.

Data Type

name: dataType, type: Enum, default: int8

Set the desired data type here.

Values:

Title

Name

​int8

​int8

​unsigned int8

​unsigned int8

​int16

​int16

​unsigned int16

​unsigned int16

​int32

​int32

​unsigned int32

​unsigned int32

​float

​float

​double

​double

​int64

​int64

​unsigned int64

​unsigned int64

​complexf

​complexf

​complexd

​complexd

​quaternionf

​quaternionf

​quaterniond

​quaterniond

​vec2

​vec2

​vec3

​vec3

​vec4

​vec4

​vec5

​vec5

​vec6

​vec6

​vec7

​vec7

​vec8

​vec8

​vec9

​vec9

​vec10

​vec10

​vec16

​vec16

​vec32

​vec32

​vec64

​vec64

​mat2

​mat2

​mat3

​mat3

​mat4

​mat4

​mat5

​mat5

​mat6

​mat6

​matf2

​matf2

​matf3

​matf3

​matf4

​matf4

​matf5

​matf5

​matf6

​matf6

​vecf2

​vecf2

​vecf3

​vecf3

​vecf4

​vecf4

​vecf5

​vecf5

​vecf6

​vecf6

​vecf7

​vecf7

​vecf8

​vecf8

​vecf9

​vecf9

​vecf10

​vecf10

​vecf16

​vecf16

​vecf32

​vecf32

​vecf64

​vecf64

Set data type

name: setDataType, type: Bool, default: FALSE

If checked, the output image is set to the indicated type, and the expression is evaluated over that type. Keep in mind that mixing incompatible types and expressions can produce very odd results.

Info

name: statusBar, type: String, persistent: no

When the expression is invalid or an error occurred during evaluation, an error message is shown here.

Update Mode

name: updateMode, type: Enum, default: AutoUpdate, deprecated name: autoUpdate

Set the desired behavior when the input images change.

Values:

Title

Name

Deprecated Name

Description

​Auto Clear

​AutoClear

​FALSE

​The output is cleared when an input image changes.

​Auto Update

​AutoUpdate

​TRUE

​The output is updated when an input image changes.

Apply Mode

name: applyMode, type: Enum, default: AutoApply

Set the desired behavior when parameter fields change. For this purpose, the following fields are parameter fields: the expression field, all variable fields, the min and max value setting fields, the data type setting field and the image extent setting field.

Values:

Title

Name

Description

​Auto Clear

​AutoClear

​The output is cleared when a parameter field changes.

​Auto Apply

​AutoApply

​The output is updated when a parameter field changes.

Update

name: update, type: Trigger

Force update with the current input images, variables and settings.

Handling on Domain Error

name: domainErrorHandling, type: Enum, default: ErrorMessage

Set what should happen when evaluation of a voxel generates a domain error. Note that the result image will always contain a 0 (or equivalent value) at the affected voxels.

Values:

Title

Name

Deprecated Name

Description

​Error Message

​ErrorMessage

​Nothing

​Print an error message. For every page with a domain error, one message is printed.

​Throw Error

​ThrowError

​Throw an error that will break page calculation and print an error message. For every page with a domain error, one message is printed.

Visible Inputs

name: numberOfInputs, type: Integer, default: 2, minimum: 0, maximum: 10

Enter number of visible input connectors.

Clear Variables

name: clearScalarVariables, type: Trigger, deprecated name: clearScalarConstants

Set all variables to zero.

Expression Comment

name: expressionComment, type: String

You can document the purpose of the expression here.

Comments

name: scalarVariablesComment, type: String, deprecated name: scalarConstantsComment

You can document the purpose of the variables here. This can be useful when external fields are connected.