CompoundMatrixArithmetic

MacroModule

genre	File
author	Darko Ojdanic
package	FMEwork/ReleaseMeVis
definition	CompoundMatrixArithmetic.def
see also	MatrixArithmetic, DecomposeMatrix, ComposeMatrix
keywords	matrix, matrices, arithmetic, multiplication, compound, homogeneous, affine, transformation, inverse

Purpose

Calculation of arithmetic expressions for several 4x4 matrices.

Usage

Write the expression in the typical form like this:

A*B*trans(C)*inv(D) + A*s1 - B*3.4

The module can calculate two expressions (P and Q), where the result of the first expression can be used for the second one. Multiplication of a matrix with a column vector is also possible. There are 8 matrices (A,B,…H) that may be used as an input for the calculation, 4 scalars (s1,..,s4) and two vector (v1,v2).

Details

Available operations:

Operation Name	Function
Add	A + B
Subtract	A - B
Multiply	A * B
Add scalar	A + s1
Multiply with scalar	A * s1
Multiply with vector	A * v1
Inverse	inv(A)
Transpose	trans(A)
Identity matrix	eye(A)
Negate	-A
Inverse of transformation matrix	inv_t(A)

A special inverse function is implemented for the homogeneous transformation matrices used for 3D rotations and translations, inv_t(A). If the matrix is represented as:

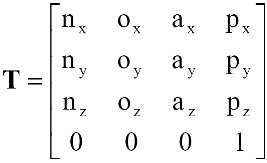
the inverse is calculated as:

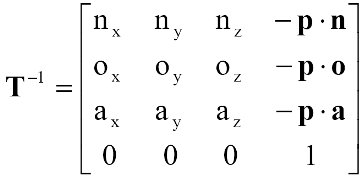
where p, n, o, a are column vectors of the matrix T, and “dot” represents scalar product.

The multiplication with the vector (e.g., A*v1) is only allowed for the column vectors, i.e., right side multiplication. Output vectors vp and vp hold the result in that case.

Scalar math functions like sqrt(),cos(),sin(), acos(), etc. or constant “pi” can be also used, as well as all other functions from the python math library. For example like this:

A*C + B*cos(pi/3)

If a pure scalar expression is given, the result appears in the corresponding output fields (sp or sq). On an empty expression, the result is the identity matrix.

Interaction

The output is updated whenever changes occur to the matrix or scalar inputs, or the field for the arithmetic expression.

Tips

The example network demonstrate a simple translation of a contour.

If you write an input matrix which is not 4x4, but for example an 5x5 matrix, no error will be reported; the result will be calculated with the first 16 elements (read as a string). So be careful, use only 4x4 matrix!

Windows

Default Panel

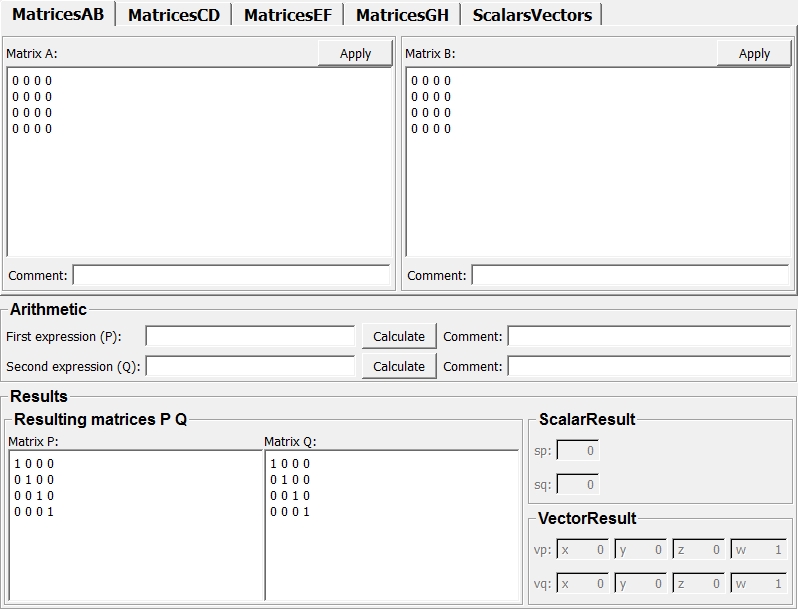
Parameter Fields

Field Index

Calculate (calcP): Trigger	First expression (P): String	resVectorQValid: Bool
Calculate (calcQ): Trigger	Matrix A: Matrix	s1: Float
Comment (expPComment): String	Matrix B: Matrix	s2: Float
Comment (expQComment): String	Matrix C: Matrix	s3: Float
Comment (matrixAComment): String	Matrix D: Matrix	s4: Float
Comment (matrixBComment): String	Matrix E: Matrix	Second expression (Q): String
Comment (matrixCComment): String	Matrix F: Matrix	sp: Float
Comment (matrixDComment): String	Matrix G: Matrix	sq: Float
Comment (matrixEComment): String	Matrix H: Matrix	v1: Vector4
Comment (matrixFComment): String	Matrix P: Matrix	v2: Vector4
Comment (matrixGComment): String	Matrix Q: Matrix	vp: Vector4
Comment (matrixHComment): String	resScalarPValid: Bool	vq: Vector4
Comment (scalarsComment): String	resScalarQValid: Bool
Comment (vectorsComment): String	resVectorPValid: Bool

Visible Fields

First expression (P)

name: expressionP, type: String

For example A*B*trans(C)*inv(D)

Second expression (Q)

name: expressionQ, type: String

For example A*B*trans(C)*inv(D)*P

Comment (expPComment)

name: expPComment, type: String

Description of expression P

Comment (expQComment)

name: expQComment, type: String

Description of expression Q

Matrix A

name: matrixA, type: Matrix, default: 0 0 0 0, 0 0 0 0, 0 0 0 0, 0 0 0 0

Provide a 4x4 matrix

Matrix B

name: matrixB, type: Matrix, default: 0 0 0 0, 0 0 0 0, 0 0 0 0, 0 0 0 0

Provide a 4x4 matrix

Matrix C

name: matrixC, type: Matrix, default: 0 0 0 0, 0 0 0 0, 0 0 0 0, 0 0 0 0

Provide a 4x4 matrix

Matrix D

name: matrixD, type: Matrix, default: 0 0 0 0, 0 0 0 0, 0 0 0 0, 0 0 0 0

Provide a 4x4 matrix

Matrix E

name: matrixE, type: Matrix, default: 0 0 0 0, 0 0 0 0, 0 0 0 0, 0 0 0 0

Provide a 4x4 matrix

Matrix F

name: matrixF, type: Matrix, default: 0 0 0 0, 0 0 0 0, 0 0 0 0, 0 0 0 0

Provide a 4x4 matrix

Matrix G

name: matrixG, type: Matrix, default: 0 0 0 0, 0 0 0 0, 0 0 0 0, 0 0 0 0

Provide a 4x4 matrix

Matrix H

name: matrixH, type: Matrix, default: 0 0 0 0, 0 0 0 0, 0 0 0 0, 0 0 0 0

Provide a 4x4 matrix

Matrix P

name: matrixP, type: Matrix, default: 1 0 0 0, 0 1 0 0, 0 0 1 0, 0 0 0 1

Result of the expression P, if the result is a matrix - otherwise a unit matrix is given.

Matrix Q

name: matrixQ, type: Matrix, default: 1 0 0 0, 0 1 0 0, 0 0 1 0, 0 0 0 1

Result of the expression Q, if the result is a matrix - otherwise a unit matrix is given.

Comment (matrixAComment)

name: matrixAComment, type: String

Description of matrix A

Comment (matrixBComment)

name: matrixBComment, type: String

Description of matrix B

Comment (matrixCComment)

name: matrixCComment, type: String

Description of matrix C

Comment (matrixDComment)

name: matrixDComment, type: String

Description of matrix C

Comment (matrixEComment)

name: matrixEComment, type: String

Description of matrix E

Comment (matrixFComment)

name: matrixFComment, type: String

Description of matrix F

Comment (matrixGComment)

name: matrixGComment, type: String

Description of matrix G

Comment (matrixHComment)

name: matrixHComment, type: String

Description of matrix H

Comment (scalarsComment)

name: scalarsComment, type: String

Description of scalars

Comment (vectorsComment)

name: vectorsComment, type: String

Description of vectors

s1

name: s1, type: Float, default: 0

s2

name: s2, type: Float, default: 0

s3

name: s3, type: Float, default: 0

s4

name: s4, type: Float, default: 0

Calculate (calcP)

name: calcP, type: Trigger

Calculate (calcQ)

name: calcQ, type: Trigger

sp

name: sp, type: Float, default: 0

Result of the expression P, if the result is a scalar - otherwise zero.

sq

name: sq, type: Float, default: 0

Result of the expression Q, if the result is a scalar - otherwise zero.

v1

name: v1, type: Vector4, default: 0 0 0 0

Provide an input vector

v2

name: v2, type: Vector4, default: 0 0 0 0

Provide an input vector

vp

name: vp, type: Vector4, default: 0 0 0 1

Result of the expression P, if the result is a vector - otherwise (0,0,0,1) is given.

vq

name: vq, type: Vector4, default: 0 0 0 1

Result of the expression Q, if the result is a vector - otherwise (0,0,0,1) is given.

Hidden Fields

resScalarPValid

name: resScalarPValid, type: Bool, default: FALSE

resVectorPValid

name: resVectorPValid, type: Bool, default: FALSE

resScalarQValid

name: resScalarQValid, type: Bool, default: FALSE

resVectorQValid

name: resVectorQValid, type: Bool, default: FALSE