QuadratureFilter

MLModule

genre	Filters
authors	Ola Friman, Mats Andersson, Hans Knutsson, Lennart Tautz, Joachim Georgii
package	FMEwork/ReleaseMeVis
dll	MLQuadratureFilter
definition	MLQuadratureFilter.def
see also	QuadratureToTensor, TensorToEigensystem
keywords	quadrature, filter, log, Gabor, normal, complex, phase, edge, energy, orientation

Purpose

The QuadratureFilter module applies a set of band-pass quadrature filters to the input image. Band-pass quadrature filters are frequently used to estimate local image features such as edges, phase, frequency, energy and orientation.

Usage

The module works on regular image data (2D or 3D). It outputs filtered image data (complex valued) and an XMarkerList containing the directions of the quadrature filters. The filter responses are stored in the u-dimension.

Details

The module applies a set of Log-Normal (also known as Log-Gabor) quadrature filters. A set contains several quadrature filters, where each filter has a different orientation. Each quadrature filter measures the energy in the Fourier domain in one direction. The Log-Normal filter kernel can in the Fourier domain be expressed as a polar separable function

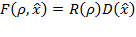
where ρ is the radial distance and x̂ is a unit vector. The name Log-Normal refers to the radial function, which has the form of a Normal or Gaussian curve on a logarithmic scale:

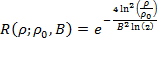
where ρ₀ is the center frequency of the band pass filter and B is the (relative) bandwidth. The bandwidth is in this module fixed to B=2. The plot below shows three different radial functions for the center frequencies 2π/8 (blue), 3π/8 (green) and 4π/8 (red).

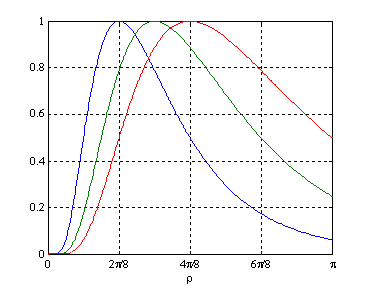
For negative frequencies the radial function is zero. That is, the quadrature filters are not symmetric in the Fourier domain and therefore complex valued in the spatial domain. The angular part has the form of a cos²() function which can be expressed as the following inner product

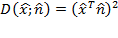
where n̂ is the direction of the filter in 2D or 3D space (or higher). Below, the Fourier domain functions of three 2D Log-Normal filters with B=2 and

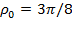
are shown. These filters have the directions

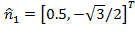
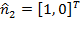
and

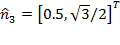
respectively.

It is critical that the quadrature filters have zero DC level. Therefore, to obtain optimal performance, the filter kernels in this module have been pre-optimized numerically to fit the ideal filter functions in the Fourier domain and to have as compact spatial support as possible. The following formulas can be used to determine a suitable filter center frequency and bandwidth. Say we want to detect objects in an image that are between x₁ and x₂ voxels large. The center frequency is then set to the geometric mean of the frequency range we want to detect:

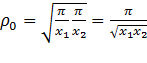
Inserting this center frequency in the radial function above, we can find the bandwidth B with which the radial response decays to 0.5 at the limits p/x₁ and p/x₁. We then get the following formula for B:

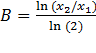
For example, if we want to detect objects between 2 and 8 voxels, we would choose a center frequency of p/4 and a bandwidth of 2.

Windows

Default Panel

Input Fields

The module takes an image volume as input. Note that the filters operate only in 2D or 3D. If 2D filtering is chosen and a 3D volume is connected to the module, each slice will be filtered separately. Note also that the module stores the filter outputs in the u-dimension. Input data in the u-dimension will therefore be ignored and overwritten.

input0

name: input0, type: Image

The input image that should be filtered.

Output Fields

The module has two outputs. The first delivers the filtered images, which are stored in the u-dimension and which are complex valued. The second output is an XMarkerList with the directions of the filters in the chosen filter set.

output0

name: output0, type: Image

The filter response. The response is always complex-valued and stores the responses for the different filter directions in the u dimension.

outputFilterDirs

name: outputFilterDirs, type: MLBase

This list contains the direction vectors of the applied filter.

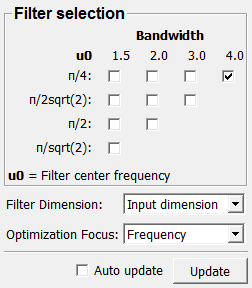
Parameter Fields

Field Index

Auto Update: Bool	B30 upi 2sqrt2: Bool
B15 upi 2: Bool	B30 upi 4: Bool
B15 upi 2sqrt2: Bool	B40 upi 4: Bool
B15 upi 4: Bool	Filter Dimension: Enum
B15 upi sqrt2: Bool	Optimization Focus: Enum
B20 upi 2: Bool	Update: Trigger
B20 upi 2sqrt2: Bool
B20 upi 4: Bool

Filters are available in pre-defined pairs of center frequency and bandwith. A lower center frequency means more smoothing.

	Bandwidth B
Center frequency ρ₀	1.5	2.0	3.0	4.0
π/4	2.4 - 6.7	2.0 - 8.0	1.4 - 11	1.0 - 16
π/(2√2)	1.7 - 4.6	1.4 - 5.7	1.0 - 8	–
π/2	1.2 - 3.4	1.0 - 4.0	–	–
π/(√2)	0.8 - 2.4	–	–	–

Visible Fields

B40 upi 4

name: B40_upi_4, type: Bool, default: TRUE

Filter with bandwidth 4 and center frequency π/4.

B30 upi 4

name: B30_upi_4, type: Bool, default: FALSE

Filter with bandwidth 3 and center frequency π/4.

B30 upi 2sqrt2

name: B30_upi_2sqrt2, type: Bool, default: FALSE

Filter with bandwidth 3 and center frequency π/(2√2).

B20 upi 4

name: B20_upi_4, type: Bool, default: FALSE

Filter with bandwidth 2 and center frequency π/4.

B20 upi 2sqrt2

name: B20_upi_2sqrt2, type: Bool, default: FALSE

Filter with bandwidth 2 and center frequency π/(2√2).

B20 upi 2

name: B20_upi_2, type: Bool, default: FALSE

Filter with bandwidth 2 and center frequency π/2.

B15 upi 4

name: B15_upi_4, type: Bool, default: FALSE

Filter with bandwidth 1.5 and center frequency π/4.

B15 upi 2sqrt2

name: B15_upi_2sqrt2, type: Bool, default: FALSE

Filter with bandwidth 1.5 and center frequency π/(2√2).

B15 upi 2

name: B15_upi_2, type: Bool, default: FALSE

Filter with bandwidth 1.5 and center frequency π/2.

B15 upi sqrt2

name: B15_upi_sqrt2, type: Bool, default: FALSE

Filter with bandwidth 1.5 and center frequency π/(√2).

Filter Dimension

name: filterDim, type: Enum, default: Input dimension

Dimension of the filter directions.

Values:

Title	Name	Description
Input dimension	Input dimension	Filter dimensions will be set to the image dimensions.
2d	2D	A 2D filter set will be used.
3d	3D	A 3D filter set will be used.

Optimization Focus

name: filterFocus, type: Enum, default: Frequency

Use a filter set optimized for either frequency or spatial domain.

Values:

Title	Name	Description
Frequency	Frequency	Filter set optimized for frequency domain.
Spatial	Spatial	Filter set optimized for spatial domain.

Update

name: updateButton, type: Trigger

Update the filter.

Auto Update

name: autoUpdate, type: Bool, default: FALSE

If checked, updates when the inputs change.