Vesselness

MLModule

genre	Filters
author	Ola Friman
package	FMEstable/ReleaseMeVis
dll	MLGaussFiltersStable
definition	MLGaussFiltersStable.def
see also	GaussHessian, itkHessian3DToVesselnessMeasureImageFilter, TensorToEigensystem
keywords	vesselness, lineness, structure, Hessian, prolate, tensor, eigenvalue

Purpose

The module Vesselness calculates a multi-scale vesselness measure, i.e., each voxel in the output volume indicates how similar the local structure is to a tube.

Details

The vesselness measure is calculated as a function of the Hessian matrix. Specifically, the eigenvalues λ₁ > λ₂ > λ₃ describe the local neighborhood.

Assuming that we want to detect bright vessels on a dark background, the eigenvalues must have the following relation: λ₁ ≈ 0 and 0 >> λ₂ ≈ λ₃. A vesselness function f(λ₁, λ₂, λ₃) measures how well this condition is fulfilled. Sato et al. uses the following function:

f(λ₁, λ₂, λ₃) = 0 if λ₂ ≥ 0,

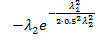
if λ₂ < 0 and λ₁ < 0,

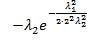
if λ₂ < 0 and λ₁ > 0.

This measure is also calculated by the ITK module itkHessian3DToVesselnessMeasureImageFilter. The same formula can be used for calculating a 2D vesselness measure. Note that the Sato et al. measure is dependent on the line contrast through the multiplication of λ₂. To normalize the vesselness measure across scale, the actual output is scaled with σ², where σ is the width of the Gaussian function used for calculating the Hessian matrix. For more information on the scaling and the calculation of the Hessian, see the help for the GaussHessian module.

An additional normalized vesselness measure is available for 2D and 3D as follows:

2D:

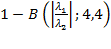
where B(x;4,4) is the incomplete Beta function with parameters 4 and 4.

3D:

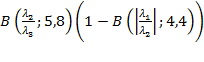
As only ratios of eigenvalues are used to calculate the normalized vesselness measure, it is contrast independent with a range between 0 and 1. The vesselness measure can be calculated over several scales. The maximum vesselness over the scales is then given as output.

Windows

Default Panel

Input Fields

input0

name: input0, type: Image

Scalar image data

input1

name: input1, type: Image

Scalar mask where all non-zero values mark an object.

Output Fields

output0

name: output0, type: Image

Image with values indicating the vesselness of voxels.

Parameter Fields

Field Index

2D calculation: Bool	Use normalized measure: Bool
Auto update: Bool
Dark vessels: Bool
Lower Sigma: Double
Number Of Scales: Integer
Sigma Unit: Enum
Update: Trigger
Upper Sigma: Double

Visible Fields

Lower Sigma

name: startSigma, type: Double, default: 1

Sets the finest scale. Sigma refers to the Gaussian filters used for estimating the Hessian matrix.

Upper Sigma

name: endSigma, type: Double, default: 2

Sets the coarsest scale. Sigma refers to the Gaussian filters used for estimating the Hessian matrix.

Number Of Scales

name: nbrOfScales, type: Integer, default: 1

Sets the number of scales used for calculating the vesselness.

The sigmas for the scales are evenly distributed between the lower and upper sigmas.

Sigma Unit

name: unit, type: Enum, default: voxel

Defines the unit for sigma.

Values:

Title	Name
voxel	voxel
mm	mm

2D calculation

name: calc2D, type: Bool, default: FALSE

If checked, the module computes the vesselness only on 2D slices (x/y plane).

Use normalized measure

name: normalizedMeasure, type: Bool, default: FALSE

If checked, the normalized vesselness measure is used, otherwise the Sato et al. measure is used.

Dark vessels

name: darkVessels, type: Bool, default: FALSE

If checked, the vessels are assumed dark on a brighter background.

Otherwise, the vessels are assumed bright on a dark background.

Update

name: update, type: Trigger, deprecated name: calcButton

If pressed, the module computes anew.

Auto update

name: autoUpdate, type: Bool, default: FALSE

If checked, the module computes anew on any parameter or input change.