SmolyakInterpolationPolynomial¶
-
MLModule¶
Purpose¶
The module SmolyakInterpolationPolynomial creates a multidimensional, scalar interpolation polynomial (i.e. a function from a multidimensional space to a one-dimensional space).
In contrast to the TensorInterpolationPolynomial module, the interpolation mesh is not a tensor product mesh, but given by the Smolyak algorithm with the Chebyshev extremum points.
See Smolyak, Soviet Math. Dokl., 1963 or Xiu/Hesthaven, SIAM J. Sci. Comput. 2005 for details.
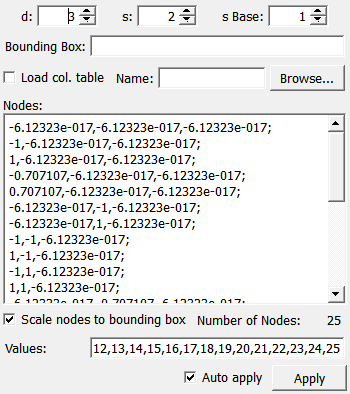
Roughly, the interpolation grid is controlled by the space dimension d and a parameter s. It is a sparse sub-grid of a tensor product grid that has 2s + 1 nodes in each direction (except for s=0, where it as only one node instead of two per direction).
Tips¶
Use of a Too Large Collocation Table¶
Sometimes, you might have performed experiments with certain values for d and s (say, d=3 and s=4, which requires 177 function evaluations), and you might want to simulate the result that would be obtained for the same layout but a smaller value for s (say, s=2). Instead of manually extracting the required 25 of the 177 computed values, this module offers an easy solution to this scenario: Enter all 177 computed values, and set s to 2, but load the external collocation table that was used with s=4 to compute the values, and set s Base to 4. The module will then automatically select the correct values.
Parameter Fields¶
Field Index¶
Apply: Trigger |
s: Integer |
Auto apply: Bool |
s Base: Integer |
Bounding Box: String |
Scale nodes to bounding box: Bool |
d: Integer |
Values: String |
Load col. table: Bool |
|
Name: String |
|
Nodes: String |
|
Number of Nodes: Integer |
Visible Fields¶
s¶
-
name:s, type:Integer, default:1, minimum:0¶ Sets a parameter that controls the number of interpolation nodes.
s Base¶
-
name:sBase, type:Integer, default:1, minimum:0¶ Sets the value of
sthat the nodes of an externally loaded collocation table are interpreted to originate from.Since setting this value to a smaller value than the s field does not make sense, the value is internally set equal to s in that case. Setting this value to a larger value than the s field will never do something wrong, but in most cases not be necessary. It is only necessary if, for some reason, you external collocation does not match the value of s that you have selected.
Bounding Box¶
-
name:boundingBox, type:String, default:-1,1¶ Sets the pre-image bounding box.
By default, the interpolation points are arranged within the cuboid [-1,1]d, where d is the space dimension.
If you want them to be arranged differently, enter a bounding box here. Separate directions by semicolon. Separate min and max values for each direction by comma. E.g., 0,1;3,4 means [0,1]x[3,4]. If you enter too many intervals (i.e., more than required by the space dimension), the last intervals will be ignored. E.g., with d=2, entering 0,1;3,4;2,5 will still mean [0,1]x[3,4]. If you enter too few intervals, they will be repeated cyclically. E.g., with d=5, entering only 0,1;3,4 will mean [0,1]x[3,4]x[0,1]x[3,4]x[0,1]. If left empty completely, the default [-1,1]d will apply.
Nodes¶
-
name:nodes, type:String, persistent:no¶ Shows the nodes as they are defined by d, s, and (if enabled) the external collocation table.
Note that the collocation table should only change the order of the nodes, nothing else. If it does, this indicates that the collocation table either does not match the given numbers d and s or does not have the required format.
Values¶
-
name:values, type:String, default:0¶ Sets the values that you would like the polynomial to take at the interpolation nodes.
Separate them with a comma. Order them in the same way as the nodes are ordered in the
Nodesfield. Note that you can influence this order by loading an external collocation table.
Scale nodes to bounding box¶
-
name:showScaledNodes, type:Bool, default:TRUE¶ If checked, the
Nodesfield displays the nodes as they are used.If unchecked, the
Nodesfield displays the nodes in an unscaled manner, i.e. arranged within the cuboid [-1,1]s, no matter what the actual bounding box is. Note that this does not change the polynomial, but only the list displayed in theNodesfield.
Load col. table¶
-
name:loadColTable, type:Bool, default:FALSE¶ If checked, an external collocation table will be loaded.
The only use of this is to determine the order of the interpolation nodes. The collocation table must be an ASCII file consisting of numbers that are separated by whitespace. The first number is ignored. After that, a list of the (unscaled) collocation nodes follows, where each node is represented by d+1 numbers. The first d numbers represent the coordinates of the collocation node, and the (d+1)st numbers is ignored.
Name¶
-
name:colTableName, type:String¶ Sets the file name of the collocation table to be loaded.
The only use of this is to determine the order of the interpolation nodes. The collocation table must be an ASCII file with the following structure: The first line contains one number only. This number will be ignored. All the following lines represent one interpolation node. They consist of d+1 numbers (where d is the space dimension, that must match the value entered in the d field). The first d numbers give the coordinates of the current interpolation node. They are always treated as unscaled, i.e. arranged within the cuboid [-1,1]d The (d+1)th number is ignored.